（１）規矩術とは

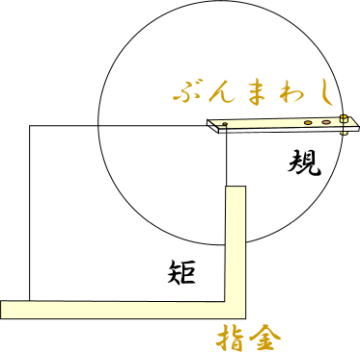
規矩術は、指金、定規、ぶんまわし（＝コンパス）などを用いて、建築物の構成や構造部分の形状を立体幾何学的に求め、部材の上に割り付け、作図する方法である。 規矩術の規は円でぶんまわし、矩は直角で指金を示している。 規矩術の原型は、指金に裏目が登場した１２世紀頃にはあったものと考えられるが、和算の影響を受けながら大工技術として完成させたのは、江戸時代も後半のことである。1788年には、「溝口流規矩術全書」と呼ばれる「方圓順度（ほうえんじゅんど）」が、東都工匠長官であった溝口内匠源林卿によって著わされている。 さらに幕府作事方大棟梁であった平内廷臣（1799〜1856）は、和算家から大棟梁になったが、1833年「匠家矩術要解」、1848年「匠家矩術新書」という二つの規矩術書を刊行し、汎用性ある現代に通じる規矩術を完成させた。 伝統的なものであると考えられている規矩術の歴史はそれほど長くはない。規矩術が盛んになったのは明治以降のことであり、多くの規矩術書が出版されている。古い規矩術には、洋小屋など作図法が載っており、当時の匠達が西洋建築に対応するために、新たな規矩術に挑戦していた様子がうかがえる。 規矩術の基本は、和算の勾股弦にある。これは三平方の定理（ピタゴラスの定理）とその応用問題である。勾股弦は２０００年程前の漢の時代に中国でまとめられた数学書「九章算術」に、勾股章として取り上げられている。わが国では１６００年に「勾股」という和算書がまとめられている。

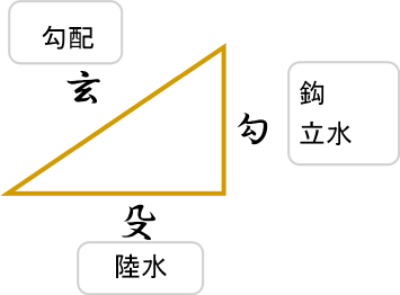
規矩術では、勾股弦を勾殳玄と表している。とくに殳は読み方さえもわからない。玄は読めるがなぜ玄なのかがわからない。 しかし股ならば、「こ」と読むことができるし、股を広げたところから底辺を指すことも想像できる。 また弦ならば、弓のつるから三角形の斜辺を思い浮かばせることができる。 勾は鉤（こう）からきており、鉤（かぎ）の手といった意味で直角を持つ辺を示している。 勾（こう）は、直角三角形の立辺のことで、鉤（かぎ）、立ち上がり、立水（たてみず）とも呼ばれる。 股（こ）は、底辺で規矩術では殳（こ）、陸水（ろくみず）とも呼ばれる。 弦（げん）は斜辺で、玄（げん）、勾配、延びがねともいう。

（２）規矩術では勾配で角度を出す

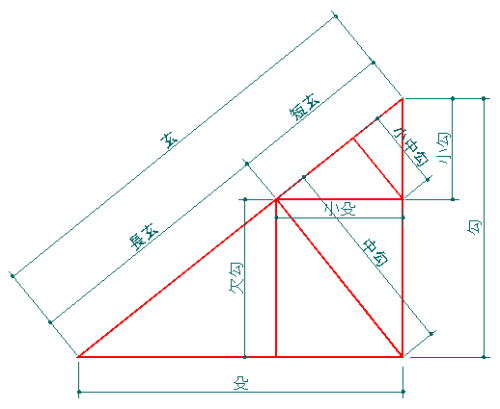
規矩術は、直角三角形が基本となっている。直角の頂点から、その対辺に下ろした垂線を、中勾、さらに下ろされた新たな頂点から、垂線を下ろし欠勾、小殳と名づけている。さらに小殳、小勾の直角三角形から玄に下ろした垂線を小中勾、対応した斜辺を短玄と名づけている。

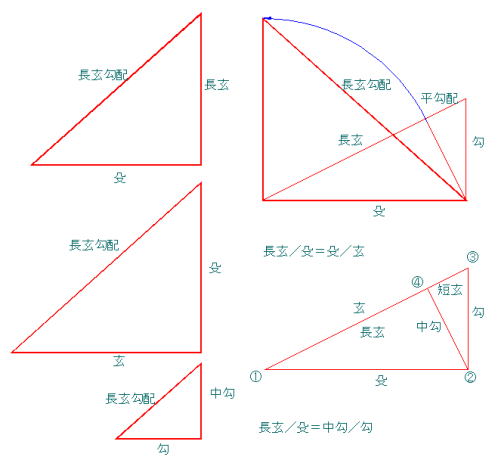
底辺を殳として、もう一辺を長玄とした勾配を、長玄勾配というように、さまざまな勾配が角度を出すために使われる。長玄の長さは基本直角三角形を書いて計ることによって出すこともできるが、規矩術が考案された時代には、すでに和算で計算によって出すことができたので、当時から例えば４寸勾配（殳が１０寸、勾が４寸）の場合の、長玄は９．２８５寸だということは出されていたはずだ。 とは言っても、建築大工の技能検定では、基本直角三角形を描くことになっているので、基本直角三角形から殳、長玄を指金で計り長玄勾配を引くといった方法も取られていたとも言える。

（３）直交座標系よりは効率よく正確に勾配が指定できる指金

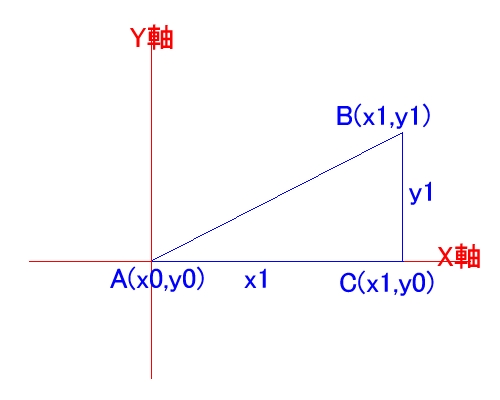
X軸（AC)に対して一定の角度を持ったABという線を引く場合について考えて見ることにする。われわれが普段製図などで用いている方法は、�@A点を通る水平線を引く、�AA点から距離ｘ１にあるC点にマーキングする、�BC点から垂線を引く、�CC点から距離ｙ１にあるB点にマーキングする、�DA点、B点に線を引くといった５工程になる。

いっぽう指金（さしがね）の場合は、�@A点を通る水平線を引く、�A指金の長手にｘ１、短手にｙ１を取り水平線に当てる、�B指金の長手に線を引くといった３工程で済んでしまう。A点、B点、C点といったマーキングが不要なので、スピードも速いし、誤差も少なくなる。 点をマーキングする必要がないので、ケガキ用のポンチのような工具が不要で、指金と墨差しだけで墨出しが可能になっている。

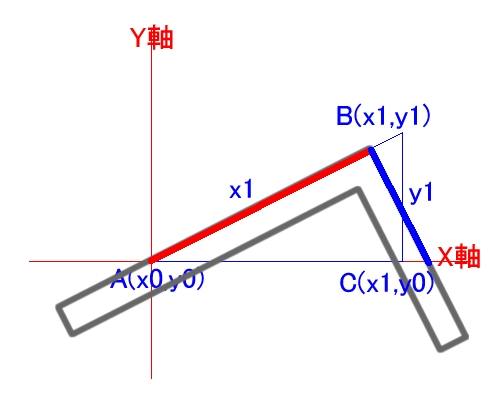指金の長手にｘ１、短手にｙ１をとった直角三角形は、直角三角形ＡＢＣと鋭角を共有しているので、相似形となる。これが指金の使い方の基本になっている。